Practice Session 3 – Chord Tones

Guitar Practice Session 3 – Chord tones in the key of C major

In the first two practice sessions we used the common I-IV-V chord progression in C major to practice playing chord tones. Now we will do the same thing again but use all of the (triad) chords in the key. The diagrams show the chord tones based around the third fret like the previous session. No TABS have been created for this session, the same idea applies, just learn the patterns in the diagrams below and play around with them over the chord progression to try and create melodic phrases.

The practice track is in the key of C major and steps through the chords in turn every two bars. The chord sequence is looped as follows.

C / Dm / Em / F / G / Am / Bdim – start over.

Get the jam track here

The patterns for the C, F and G chords were covered in session 1 but I’ll repeat them here again for quick reference. Learn the notes as well as the interval relationships.

Chord patterns and notes.

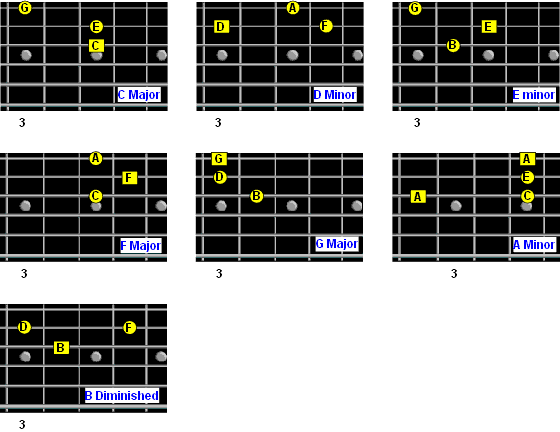
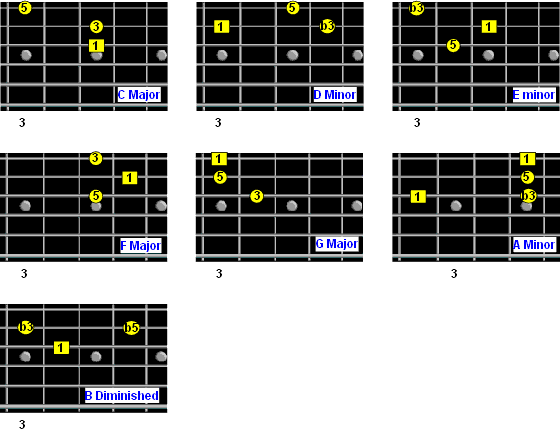
Chord patterns showing intervals